Background and Motivation

Accurate representation of dynamic flow stress is essential for predicting material behaviour under high strain-rate loading. Widely used decoupled empirical models, such as the Johnson-Cook (J-C) equation, assume that the effects of strain, strain-rate, and temperature can be factorized. However, the mathematical legitimacy of this assumption and its consistency with discrete experimental data have not been rigorously examined.

Conventional fitting approaches often rely on sequential calibration procedures and limited subsets of experimental data, which may obscure the intrinsic data structure and lead to unreliable constitutive representations, especially when coupling effects are significant.

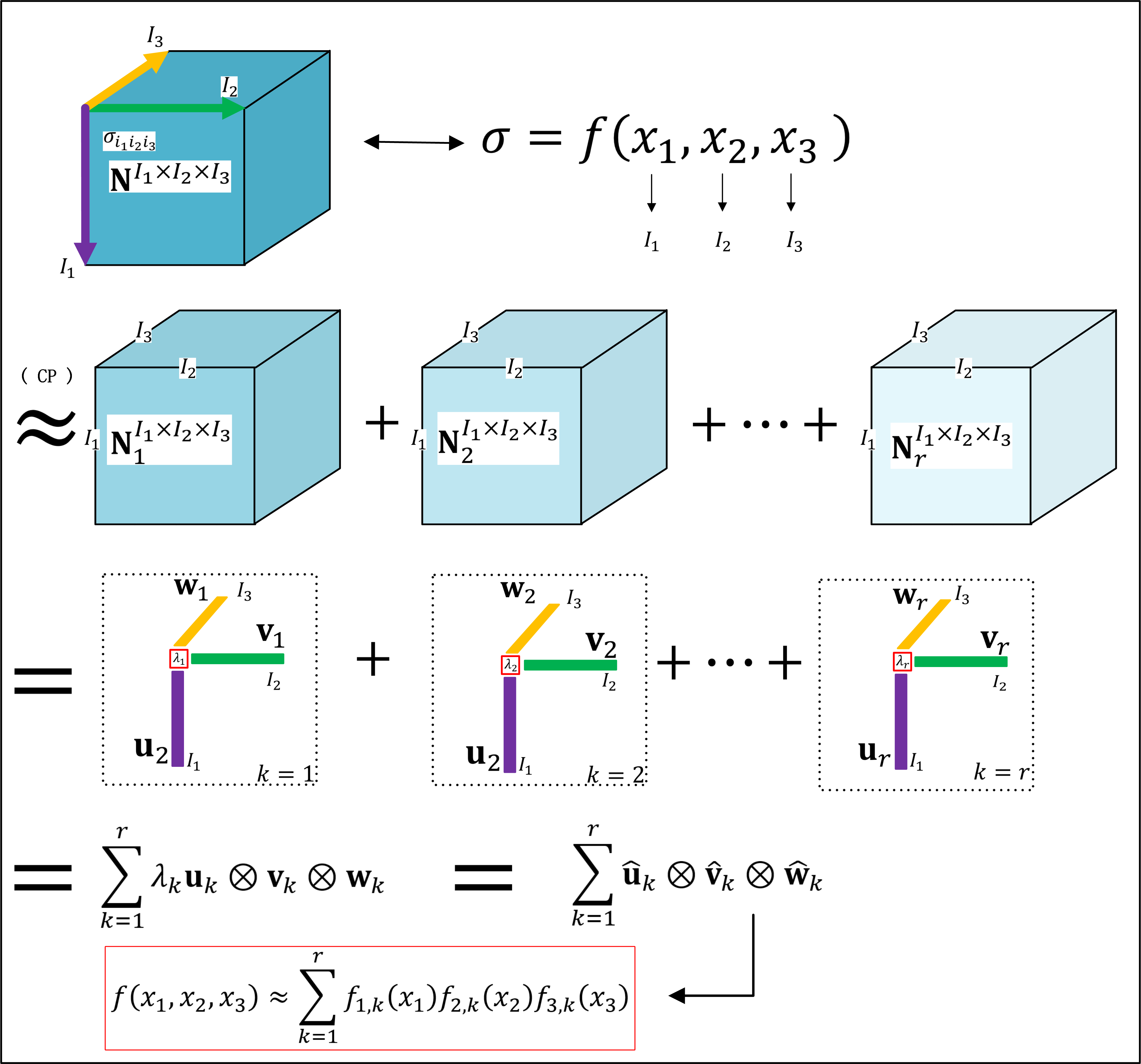
Motivated by these limitations, this work introduces a data-driven framework based on matrix and tensor decomposition to reveal the intrinsic structure of dynamic flow stress data. The study establishes a quantitative criterion for the validity of decoupled flow stress equations and provides a robust method for representing dynamic flow stress directly from discrete experimental datasets.

Highlights

• Dynamic flow stress data structure is revealed using SVD/CP decomposition methods;
• Discrete flow stress representation method is established;
• The legitimacy of decoupled (factorized) flow stress equations is mathematically verified;
• The problems associated with Johnson-Cook flow stress equation is clarified;
• A reliable method for the representation of dynamic flow stress is developed and demonstrated

Source: Xianglin Huang, Q.M. Li, The legitimacy of decoupled dynamic flow stress equations and their representation based on discrete experimental data, International Journal of Impact Engineering, Volume 173, 2023, 104453, ISSN 0734-743X, https://doi.org/10.1016/j.ijimpeng.2022.104453.